Mi a tangens a körhöz? A kör érintő tulajdonságai. A két körhöz tartozó közös érintő

Secs, tangens - mindez több száz alkalommal hallott a geometria leckékén. De az iskolából végzett iskolai végzettség, az évek elteltével, és ez a tudás elfelejtett. Mit kell emlékezni?

lényeg

A "tangens a körhöz"valószínűleg mindenkinek. De alig mindenki képes lesz gyorsan megfogalmazni meghatározását. Eközben az érintő egy egyenes vonal, amely egy síkban fekszik, és egy körrel csak egy pontra metszik. Rengeteg közülük lehet, de mindegyiküknek ugyanazok a tulajdonságai vannak, amelyeket alább tárgyalunk. Nem nehéz kitalálni, hogy a tangenciális pont az a hely, ahol a kör és a vonal metszi. Mindegyik esetben ez egy, de ha több van, akkor már lesz szekunder.

A felfedezés és a tanulmány története

Az érintő koncepciója az ősi időkben jelent meg. Ezeket az egyenes vonalakat először a körhöz, majd az ellipszishez, a parabolákhoz és a hiperbolákhoz egy vonalzó és egy iránytű segítségével végeztük el a geometria fejlődésének kezdeti szakaszában is. Természetesen a történelem nem tartotta fenn a felfedező nevét, de nyilvánvaló, hogy még akkor is az emberek tudták a kerületi érintőt.

Az Új Idõben ez a jelenség érdeklõdöttismét - új koncepció tanulmányozása kezdődött az új görbék felfedezésével összefüggésben. Tehát a Galileo bevezette a cikloid fogalmát, és Fermat és Descartes tangentumot építettek hozzá. Ami a köröket illeti, úgy tűnik, hogy még az ősök számára sem volt titok ezen a területen.

tulajdonságok

A keresztezési ponton levő sugár merőleges az egyenes vonalra. Ez így van

fő, de nem az egyetlen tulajdonság, amiérintődik a körhöz. Egy másik fontos jellemzője két egyenes vonal. Tehát a körön kívül eső ponton két érintőt húzhat meg, és szegmenseik egyenlőek lesznek. Van egy másik tétel ebben a témában, de ritkán keretében megrendezésre került a hagyományos iskolai persze, de ez rendkívül hasznos bizonyos problémák megoldásában. Ez így hangzik. A körön kívül eső egyetlen ponttól rajzolódik egy érintő és egy szekvencia. AB, AC és AD szegmensek vannak kialakítva. A - a vonalak metszéspontjába, B az érintési pont, C és D - keresztezési. Ebben az esetben a következő egyenlet érvényes: a hossza a kör érintője, négyzetes, megfelel a termék a szegmensek AC, AD.

A fentiekből fontos következmény van. A kör minden pontján meg lehet szerkeszteni a tangent, de csak egyet. Ennek bizonyítása meglehetősen egyszerű: elméletileg a merőleges a sugárról lefelé esik, és kiderül, hogy a kialakult háromszög nem létezhet. Ez azt jelenti, hogy az érintő egyedülálló.

épület

A geometriai problémák között egyébként is van egy speciális kategória, általában nem

szerető diákok és diákok. A feladatok ebből a kategóriából történő megoldásához csak az iránytű és a vonalzó szükséges. Ezek építési feladatok. Vannak ott, és egy érintő szerkezete.

Szóval, egy kör és egy pont kívül fekvehatárokat. És érdemes rajzolni egy érintőt. Hogyan lehet ezt tenni? Először is egy szegmenst kell rajzolnunk az O kör és az adott pont középpontja között. Ezután az iránytű használatával fel kell osztania. Ehhez meg kell adnia egy sugár - az eredeti kör középpontja és az adott pont közötti távolságnak csaknem felét. Ezt követően két egymást keresztező ívet kell létrehoznunk. És az iránytű sugara nem szükséges megváltoztatni, és a kör minden egyes részének középpontja a kezdőpont és az O. Az ívek metszéspontjait össze kell kötni, ami fel fogja osztani a szegmenst. Állítsa be az iránytűnek megfelelő távolságot. Ezután, a kereszteződési pont közepén, készítsen másik kört. Ez tartalmazza az eredeti pontot és az O-t is. A probléma két további kereszteződést tartalmaz az adott körrel. Ezek az eredetileg meghatározott pont pontjai.

érdekes

A születéshez vezető kört érintő tangensek építése volt

differenciál kalkulus. A témáról szóló első munkát a híres német Leibniz matematikus publikálta. Elképzelte a maximumok, minimumok és tangensek megtalálásának lehetőségét, függetlenül a tört és irracionális értékektől. Nos, sok más számításra használják.

Ezenkívül a kör érintője kapcsolódikgeometriai érzéke. Ebből származik a neve. A latin tangensek fordításával - "tangens". Így ez a koncepció nem csak a geometriával és a differenciál kalkulussal, hanem a trigonometria is kapcsolódik.

Két kör

Nem mindig az érintő csak egy számot érint. Ha hatalmas számú egyenes vonalat húzhat egy körre, akkor miért nem fordítva? Tudod. Ez csak a probléma ebben az esetben komolyan bonyolult, mert a két kör érintése nem tud átmenni semmilyen ponton, és ezeknek a számoknak kölcsönös elrendezése nagyon

más.

Típusok és fajták

Amikor két körre és egy vagytöbb egyenes vonalat, még akkor is, ha tudjuk, hogy ezek tangensek, akkor nem azonnal világossá válik, hogy ezek az ábrák egymáshoz viszonyítva rendeződnek. Ennek alapján különbözõ fajtákat különböztetünk meg. Tehát a köröknek egy vagy két közös pontja van, vagy egyáltalán nem. Az első esetben egymást keresztezik, és a második pillanatban. És itt két fajtát különböztetünk meg. Ha az egyik kört a másodikba beágyazották, akkor az érintést belsőnek, ha nem, majd külsőnek nevezik. Az ábrák viszonylagos helyzetének megértése nemcsak a rajzon alapulhat, hanem a sugaraik összegéről és a központok közötti távolságról is. Ha ez a két mennyiség egyenlő, akkor a körök érintik. Ha az első több - keresztezi egymást, és ha kevesebb - akkor nincs közös pontja.

Tehát egyenes vonalakkal. Minden két kör számára, amelyeknek nincs közös pontja, lehet

négy tangenset alkotnak. Két közülük metszi a számokat, belsőnek nevezik őket. Még egy pár külső is.

Ha olyan körökről beszélünk, amelyeknek van egya pont komolyan egyszerűsödik. Az a tény, hogy ebben az esetben bármilyen kölcsönös megegyezés esetén az érintőnek csak egy lesz. És átmegy a kereszteződésük pontján. Tehát a nehézség megteremtése nem okoz.

Ha a számok két metszésponttal rendelkeznek, akkorszámukra a körhöz egyenes vonalat lehet kialakítani, mind az egyik, mind a második, de csak a külső. A probléma megoldása hasonló ahhoz, amit később tárgyalunk.

Problémamegoldás

Mind a belső, mind a külső érintő kétkörök, az építőipar nem olyan egyszerű, bár ez a probléma megoldódott. Az a tény, hogy ehhez egy kisegítő számot használnak, így önmagával is előállhat

meglehetősen problémás. Így két különböző sugárral és O1 és O2 központtal rendelkező köröket kapunk. Számukra két pár tangent kell létrehoznunk.

Először is, a nagyobb kör közepénKi kell építeni egy kisegítőt. Ugyanakkor a két eredeti szám sugara közötti különbséget az iránytűre kell beállítani. Egy kisebb kör középpontjától kezdve a segédkörhöz érintő tangensek épülnek fel. Ezután O1 és O2-ból merőlegesek ezek az egyenesek, mielőtt átlépnék az eredeti számokkal. Az érintő alapjellegéből az alábbiak szerint mindkét körben a szükséges pontok találhatók. A problémát legalább az első rész megoldja.

A belső tangensek kialakítása érdekében gyakorlatilag megoldást kell találni

hasonló probléma. Újból szükségünk van egy kiegészítő alakra, de ezúttal a sugara megegyezik az eredeti összegével. Ehhez a tangensek az egyik kör középpontjából épülnek fel. A megoldás további folyamata az előző példából is megérthető.

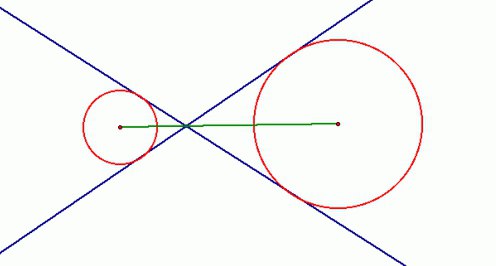
Érintse meg a kör vagy akár két vagy több -nem ilyen nehéz feladat. Természetesen a matematikusok már régóta nem tudják megoldani ezeket a problémákat manuálisan, és megbízhatják a számításokat a speciális programokhoz. De ne gondold, hogy most nem kell önmagadat csinálnod, mert a számítógépes feladatok megfelelő megfogalmazásához sokat kell tenned és értened. Sajnos féltek, hogy a végső áttérés a tudásvezérlés teszt formájára, az építési feladatok egyre több nehézséget okoznak a diákoknak.

Ami azt illeti, hogy gyakoribb tangenseket találunk több kör számára, ez nem mindig lehetséges, még akkor is, ha ugyanabban a síkban vannak. De egyes esetekben ilyen egyenes vonalat találhat.

Példák az életről

Gyakran gyakori a két körhöz tartozó tangensa gyakorlatban is megtalálható, bár nem mindig észrevehető. A szállítószalagok, a blokkrendszerek, a szíjtárcsák szállítószíjai, a varrógépben lévő szálfeszítés és még csak egy kerékpárlánc is mindegyik példája az életnek. Tehát ne gondoljuk, hogy a geometriai problémák csak elméletben maradnak: a mérnöki, fizikai, építési és sok más területen, amelyek gyakorlati alkalmazást találnak.

</ p>>